2025OpenHarmonyCTF-Crypto-WP
第一届鸿蒙CTF,密码部分都挺简单的
Ea5y_RSA
题目描述
1 | 这是一个未完全开发的OpenHarmony应用,在hint.txt中泄露了部分日志记录。请根据给定的源码和日志记录得到flag |
题目附件
思路
Ea5y_rsa.ets里面有密文: 1
nlRTOIr7P61VxeNDiPtFd65VCBJWhKlpSMF+g7Fib3VYHZYc/kgNWeFHSMvcgsqWuBCfMkB90SPQDR6hKvaxhYrqLAg/8+rRWqZbL7hXD3s2JA92V8zgx18r9zmekS28UiTUTUZDkkAhhkrWFvdx3gqgxGwj/l+DX82StHiyyOo=
hint.txt里面的gift有部分私钥: 1
00300d06092a864886f70d0101010500048202623082025e02010002818100a2f1fcc64fe2cb96aad3af057fdc9ad7fabe7d032b0fd6ef7a94af14d0adf155a85cb56edca219cd9f6077b41321093422890466a6c38ecc01f78c8db85c0ea27bd0a066709ac282688b8d0a3694a0a464f5d0292767a087636c0fe7dbfff92372836c4690b676fdde73b5479b46878d2449ddcd921f0837b52e6f7fd065b9dd02030100010281802b0d8d2048d33fbf9b7b3aef550d50cc6830148fd5bce5a978d5f83ca3b691e1740eaad193f230a727c931579f06478c42e3b909f65e0d48d1ec3a72e7974b362f59f5d3f871a2bd65bd44a8a503dd17b0b74e38b396c63f7e83dfa5ef203b9ebbcddfd3e4376b1388f1a9ce83225fe1
只能提取出1024bit的n和d的高896bit: 1
2
3e = 65537
n = 0x00a2f1fcc64fe2cb96aad3af057fdc9ad7fabe7d032b0fd6ef7a94af14d0adf155a85cb56edca219cd9f6077b41321093422890466a6c38ecc01f78c8db85c0ea27bd0a066709ac282688b8d0a3694a0a464f5d0292767a087636c0fe7dbfff92372836c4690b676fdde73b5479b46878d2449ddcd921f0837b52e6f7fd065b9dd
dh = 0x2b0d8d2048d33fbf9b7b3aef550d50cc6830148fd5bce5a978d5f83ca3b691e1740eaad193f230a727c931579f06478c42e3b909f65e0d48d1ec3a72e7974b362f59f5d3f871a2bd65bd44a8a503dd17b0b74e38b396c63f7e83dfa5ef203b9ebbcddfd3e4376b1388f1a9ce83225fe1
exp
d高位泄露攻击: 1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24# exp.sage
from Crypto.Util.number import *
from base64 import b64decode
c = 'nlRTOIr7P61VxeNDiPtFd65VCBJWhKlpSMF+g7Fib3VYHZYc/kgNWeFHSMvcgsqWuBCfMkB90SPQDR6hKvaxhYrqLAg/8+rRWqZbL7hXD3s2JA92V8zgx18r9zmekS28UiTUTUZDkkAhhkrWFvdx3gqgxGwj/l+DX82StHiyyOo='
e = 65537
n = 0x00a2f1fcc64fe2cb96aad3af057fdc9ad7fabe7d032b0fd6ef7a94af14d0adf155a85cb56edca219cd9f6077b41321093422890466a6c38ecc01f78c8db85c0ea27bd0a066709ac282688b8d0a3694a0a464f5d0292767a087636c0fe7dbfff92372836c4690b676fdde73b5479b46878d2449ddcd921f0837b52e6f7fd065b9dd
dh = 0x2b0d8d2048d33fbf9b7b3aef550d50cc6830148fd5bce5a978d5f83ca3b691e1740eaad193f230a727c931579f06478c42e3b909f65e0d48d1ec3a72e7974b362f59f5d3f871a2bd65bd44a8a503dd17b0b74e38b396c63f7e83dfa5ef203b9ebbcddfd3e4376b1388f1a9ce83225fe1
leakbit = 112 * 8
print(leakbit)
k = e * (dh << (1024 - leakbit)) // n + 1
PR.<x> = PolynomialRing(RealField(2048))
f = e * (dh << ((1024 - leakbit))) * x - x - k * (x - 1) * (n- x)
r = f.roots()
ph = int(r[0][0])
PR.<x> = PolynomialRing(Zmod(n))
f = ph + x
pl = int(f.small_roots(X=2**200, beta=0.49, epsilon=0.02)[0])
p = ph + pl
q = n // p
c = bytes_to_long(b64decode(c))
d = pow(e, -1, (p - 1) * (q - 1))
m = pow(c, d, p * q)
print(long_to_bytes(m))
Small Message For (SM4) Encryption
题目描述 1
2
3SM4 is a block cipher, standardised for commercial cryptography in China. It is used in the Chinese National Standard for Wireless LAN WAPI (WLAN Authentication and Privacy Infrastructure), and with Transport Layer Security.
It seems to be very secure... But what if someone implement it insecurely?
题目附件 1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29from gmssl import sm4, func
from os import urandom
from flag import FLAG, secret_message
def xor(a, b):
return bytes(x ^ y for x, y in zip(a, b))
def encrypt(key, plaintext, iv):
cipher = sm4.CryptSM4(sm4.SM4_ENCRYPT, 0)
cipher.set_key(key, sm4.SM4_ENCRYPT)
ciphertext = cipher.crypt_cbc(iv,plaintext)
return ciphertext
def main():
key = secret_message
while len(key) < 16:
key += secret_message
key = key[:16]
iv = urandom(16)
plaintext = b"My FLAG? If you want it, I'll let you have it... search for it! I left all of it at that place: " + FLAG
assert len(plaintext) % 16 == 0, "The message must be a multiple of 16 bytes."
ciphertext = encrypt(key, plaintext, iv)
print(f"Ciphertext: {ciphertext.hex()}")
print(f"What is this: {xor(key, iv).hex()}")
if __name__ == "__main__":
main()
exp
让ai写一个爆破secret_message的脚本 1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57from gmssl import sm4, func
import itertools
import string
# 已知数据
ciphertext_hex = "d9ea43b0d208aa168e4a275a69df3bc86051e756f9ca7959b68c6b23c9e1b69c19e08b75938375a6be830d1844d8a6e368faf1ddffecea69b5abe00ac0d6e10d6696be33d40e83a272072fbe131f98c82587011f61f2d58a020c8c54cf9b651abd740a3d55d36daa9c88cfc10a520ce4211fba4365ce98b82355b17c64dd2de4800fc68df36cfa8a3fd05baac6970dcd"
xor_key_iv_hex = "ee278c4e526ff15b8d308b6b18f83221"
# 转换为字节
ciphertext = bytes.fromhex(ciphertext_hex)
xor_key_iv = bytes.fromhex(xor_key_iv_hex)
# 可能的字符集 (可打印ASCII)
charset = string.printable.strip()
def decrypt(key, ciphertext, iv):
cipher = sm4.CryptSM4(sm4.SM4_DECRYPT, 0)
cipher.set_key(key, sm4.SM4_DECRYPT)
plaintext = cipher.crypt_cbc(iv, ciphertext)
return plaintext
def brute_force_secret_message():
# 尝试1-16字节长度的secret_message
for length in range(1, 17):
print(f"Trying length: {length}")
# 生成所有可能的组合
for candidate in itertools.product(charset, repeat=length):
secret = ''.join(candidate)
# 扩展key到16字节
key = (secret * (16 // len(secret) + 1))[:16].encode()
# 计算iv
iv = bytes(x ^ y for x, y in zip(key, xor_key_iv))
try:
plaintext = decrypt(key, ciphertext, iv)
# 检查解密结果是否符合预期格式
if b"My FLAG? If you want it" in plaintext:
print(f"Found secret_message: {secret}")
print(f"Decrypted plaintext: {plaintext}")
# 提取FLAG
flag_start = plaintext.find(b"flag{")
if flag_start != -1:
flag_end = plaintext.find(b"}", flag_start) + 1
flag = plaintext[flag_start:flag_end].decode()
print(f"FLAG found: {flag}")
return secret, flag
except:
continue
return None, None
if __name__ == "__main__":
secret_message, flag = brute_force_secret_message()
if secret_message:
print(f"Success! secret_message: '{secret_message}', FLAG: '{flag}'")
else:
print("Failed to find the secret_message and FLAG.")
Weak_random
题目描述 1
一道弱伪随机数生成器题目,密钥的生成过程存在严重漏洞。
题目附件 1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40from secret import flag
import time
import os
import random
from Crypto.Util.number import *
from Crypto.Cipher import AES
import os
import hashlib
assert(len(flag)==32)
def padding(message):
padding_len = 16 - len(message)%16
ret = hex(padding_len)[2:].zfill(2)
return bytes.fromhex(ret*padding_len)+message
def get_weak_entropy():
time_now=time.time()%10000
entropy_part1 = int(time_now) & 0xFFFF
entropy_part2 = os.getpid() & 0xFF
final_seed = entropy_part1 + (entropy_part2 << 8)
random.seed(final_seed)
key = random.getrandbits(128)
return key
entropy_key=get_weak_entropy()
iv = os.urandom(16)
key_bytes = entropy_key.to_bytes(16, byteorder='big')
msg=padding(flag.encode())
aes = AES.new(key_bytes,AES.MODE_CBC,iv=iv)
enc = aes.encrypt(msg)
print(enc.hex())
check=hashlib.sha256(flag.encode('utf-8')).hexdigest()
print(check)
#enc=e88b2eb25b22929b2eb84898bc2c620c8798637ab64b892c218c83a0e523580f6c5772c84461f09045b6bce48c102a5f
#check=83d92dc441e420587b2eb46f46ca424597af97a88f0da1b64243e287c69aa645
exp
1 | import os |
flag{9848ca46c1c1cc9db4246566b275d3c8}
Simple LLL
题目描述 1
simple lattice but openharmony
题目附件
思路
解压后发现是个鸿蒙逆向,拿https://github.com/ohos-decompiler/abc-decompiler/releases工具反编译。
核心加密如下: 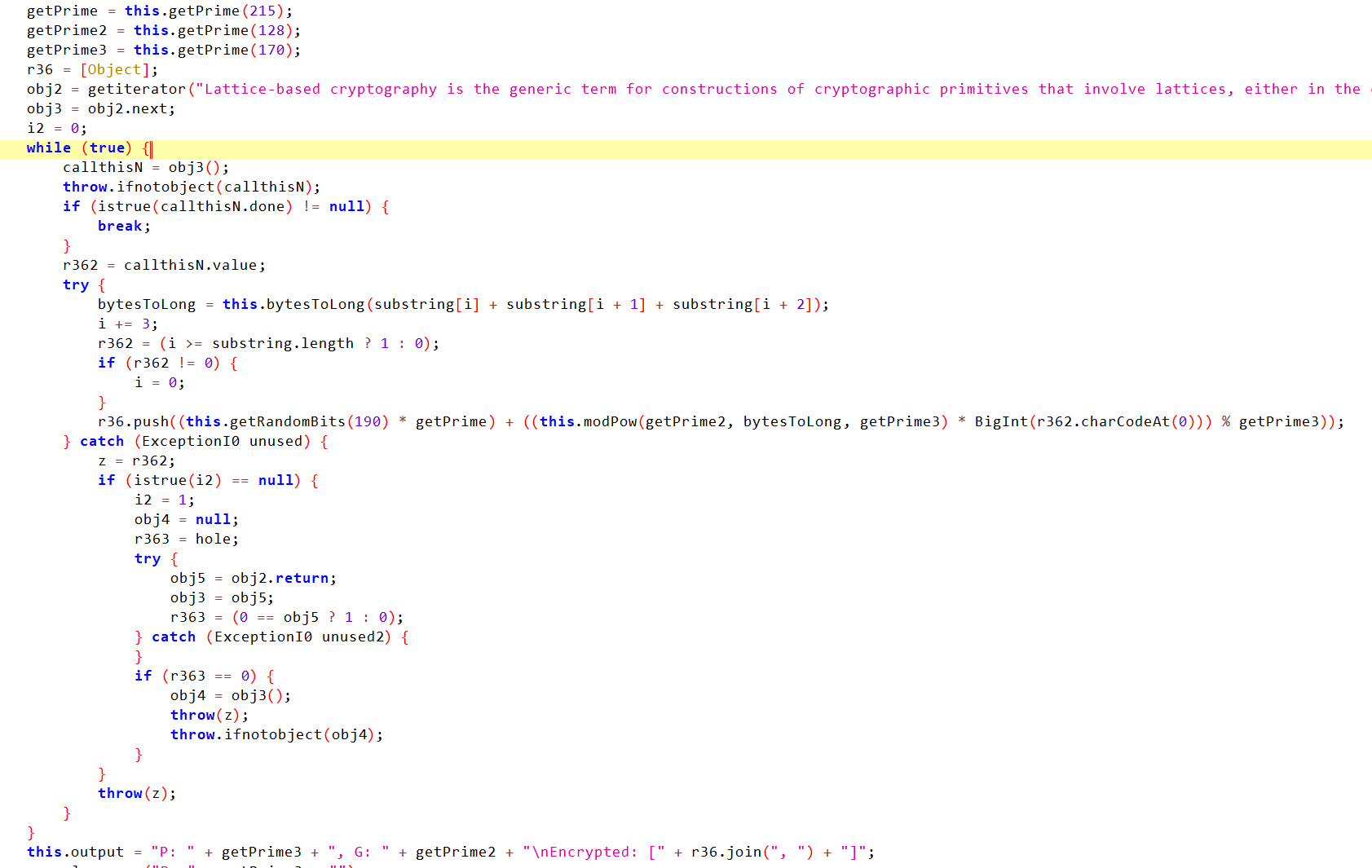
即我们可以得到50组如下形式的\(c_i\): \[ c_i = r_i*q + (g^{m_i}s_i \mod p) \] 其中\(r_i\),\(q\)相对\(p\)较小,所以直接用正交格加离散对数就解掉了
exp
1 | from Crypto.Util.number import * |
最后解出来这一串不是flag,flag是子串b8fdba363c31f3a4cadaf5289e0bf4fb578f2a5e28dcd。。。
