NepCTF2025-Crypto-WP
赛中只写了Crypto部分，最终排名No.10。
本次比赛有些题目比较特别，总体感觉是挺有趣的。
Nepsign
题目描述
1 | 来签个名吧！flag格式为NepCTF{xxx} |
题目附件
解题思路
签名由48个哈希值组成，当私钥相同时，每个位置的哈希值只与当前位置\(i\)和\(step[i]\)有关，\(step[i]\)由签名的消息确定。所以先求出happy for NepCTF 2025的\(step\)，然后随机选取一些消息发送给服务器，从返回的签名中拿到\((i,
step[i])\)对应的哈希值，需要的签名都拿到后，发给服务器就行。
exp
1 | # exp.py |
latticebros
题目描述
1 | 你能从给定的信息中找出隐藏的flag吗? flag格式为NepCTF{xxx} |
题目附件
解题思路
已知： \[ \alpha^3 + a_2\alpha^2 + a_1\alpha + a_0 = 0 \] 这里\(a_i\)都是整数，构造如下格：
\[ (1, a_2, a_1, a_0) \begin{pmatrix} \alpha^3C & 1 & 0 & 0 \\ \alpha^2C & 0 & 1 & 0 \\ \alpha C & 0 & 0 & 1 \\ C & 0 & 0 & 0 \\ \end{pmatrix}=(\epsilon C, 1,a_2, a_1) \]
由于\(\alpha\)精度有限，所以\(\epsilon\)是一个非常接近0的数。
求出\(a_2,
a_1\)后代入原来的多项式得到\(a_0\)。剩下的就是一个经典的HNP。
exp
1 | # exp.sage |
ezRSA2
题目描述
1 | Easy RSA, easy strategy. No need to brute force. |
题目附件
解题思路
\(d \approx N^{0.33}\)，上界大于\(N^{0.292}\)，但是给了\(d\)的低位，可以用来优化。 已知： \[ e(d_{m}M + d_{l}) = 1 + k(N - p - q + 1) \] 变形得： \[ ed_{m}M = 1 + k(N - p - q + 1) - ed_{l} \] 令\(X = k, Y = p + q\)，然后在模\(eM\)对如下多项式使用二元copper就行： \[ f(X, Y) = 1 + X(N - Y + 1) - ed_{l} \]
exp
1 | # exp.sage |
transistion
题目描述
1 | 我们通过一个DFF串行把数据从本机传输进FPGA里然后进行能量采集。先对时钟采样来了解一下板子的基础信息，或许我们还能从中发现一些关于transition的侧信道信息…… |
题目附件
解题思路
测试发现，一共采样了8000个数据，根据data的长度为64，推出data中的一个数据在采样中占125次，所以估计在125处附近会发生跳变，接着测试110~140的连续采样，发现在128处的采样能反映所有的跳变情况：
- \(samples[128] \leq 0.5\)，不跳变，相邻2比特是00。
- \(0.5 < samples[128] \leq 2\)，跳变，相邻2比特是01。
- \(2 < samples[128] \leq 3\)，跳变，相邻2比特是10。
- \(3 < samples[128]\)，不跳变，相邻2比特是11。
所以每次采样可以获取2比特信息，这样再以250为间隔采样，只需32次就能完全确定data，这也足够获取完整的flag。
exp
1 | # exp.py |
unloopshock
题目描述
1 | turtle 会使用AES加密你的信息，且每一个人（每一次链接）都会使用不同的KEY，你能从turtle口中泄露你的KEY吗 |
题目附件
解题思路
根据提示，关注密钥拓展部分(密钥拓展函数地址为0x01BC)：
下图已恢复部分函数名。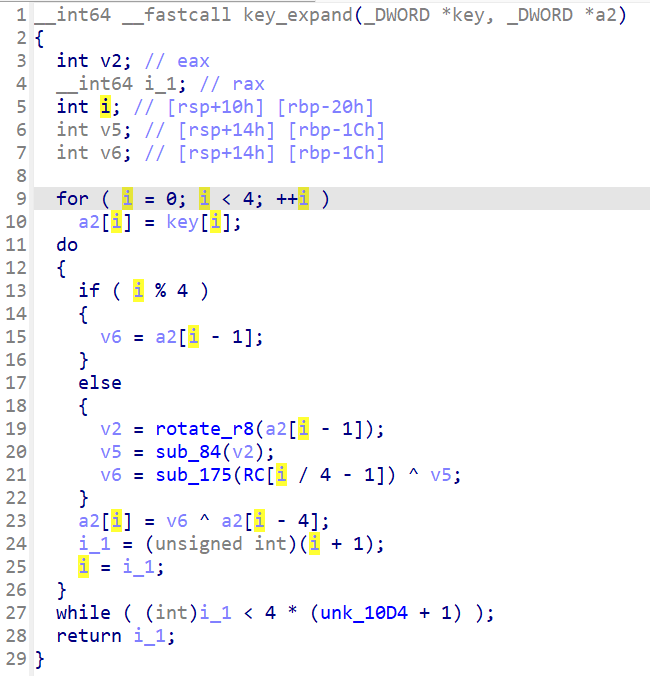 
通过查看key_expand函数的引用，可以知道a2数组用来存放拓展密钥。第一个for循环将初始密钥复制到a2中，并在接下来的do-while循环中开始密钥拓展，如果能让do-while循环不执行那么拓展的密钥只有前16字节是初始密钥，而后面全为0字节。这样就可以根据已知明密文推出初始密钥。
为了让do-while循环不起作用，可以在前面的for循环结束时，通过注入错误修改变量i的值，让i足够大且i不是4的倍数，这样在进行了一些无意义的赋值后就可以直接跳出do-while循环。
所以在汇编中找到修改变量i的地方： 
可以发现是通过将i赋值给eax，在对eax加1后再赋值给i实现的i的加1。那么可以hook
add eax 1指令，通过随机修改eax的值来改变i的值。
exp
1 | # exp.py |
*国产密码应用
题目描述
1 | 小明通过开源的GMSSL采用TLCP协议实现与服务端之间数据的传输机密性和完整性保护，且均采用服务器密码机实现数据加解密和签名验签的运算。但是在运行过程中似乎都出现了一些小问题，你能发现吗？（答案格式：NepCTF{XXX}） |
题目附件
解题思路
学了2天的TLCP，终于成功复现。
学习过程中主要参考了如下资料：
1. GB/T
32918 SM2椭圆曲线公钥密码算法：总则
2. GB/T
32918 SM2椭圆曲线公钥密码算法：数字签名算法
3. GB/T
32918 SM2椭圆曲线公钥密码算法：密钥交互协议
4. GB/T
32918 SM2椭圆曲线公钥密码算法：公钥加密算法
5. GB/T
32918 SM2椭圆曲线公钥密码算法：参数定义
6. GB/T
35276 SM2密码算法使用规范
7. GB/T
38636 传输层密码协议（TLCP）
8. bilibili-泥瓦匠的标准解读-【GB/T
38636】TLCP协议中密钥计算（手动计算主密钥、工作密钥）
9. bilibili-国密TLCP协议解析
10. csdn-预主密钥/主密钥计算和Finished消息的加解密
使用的gmssl的python实现：
11. https://github.com/py-gmssl/py-gmssl
获取签名私钥
TLCP的握手流程如下[7]：
wireshark解析的流量包：（注意低版本的wireshark不能正确显示TLCP协议，这里使用的版本为4.4.8）
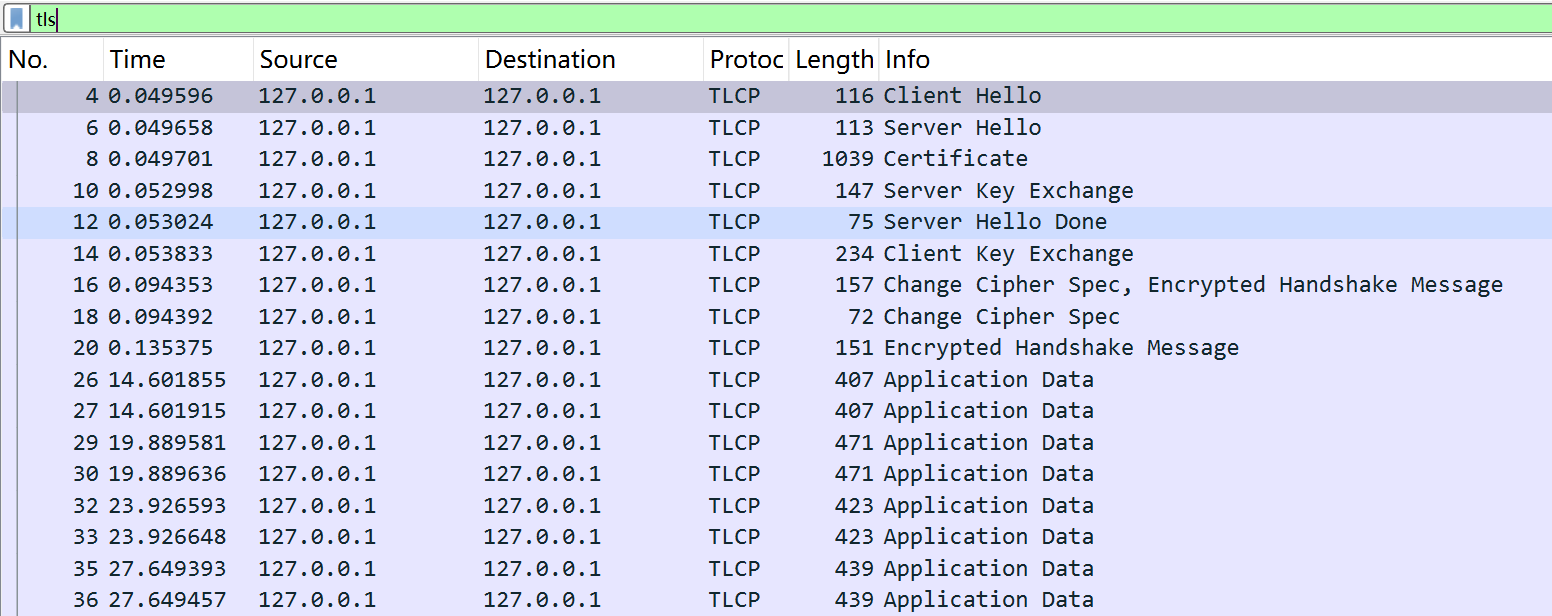
首先来看Client Hello消息：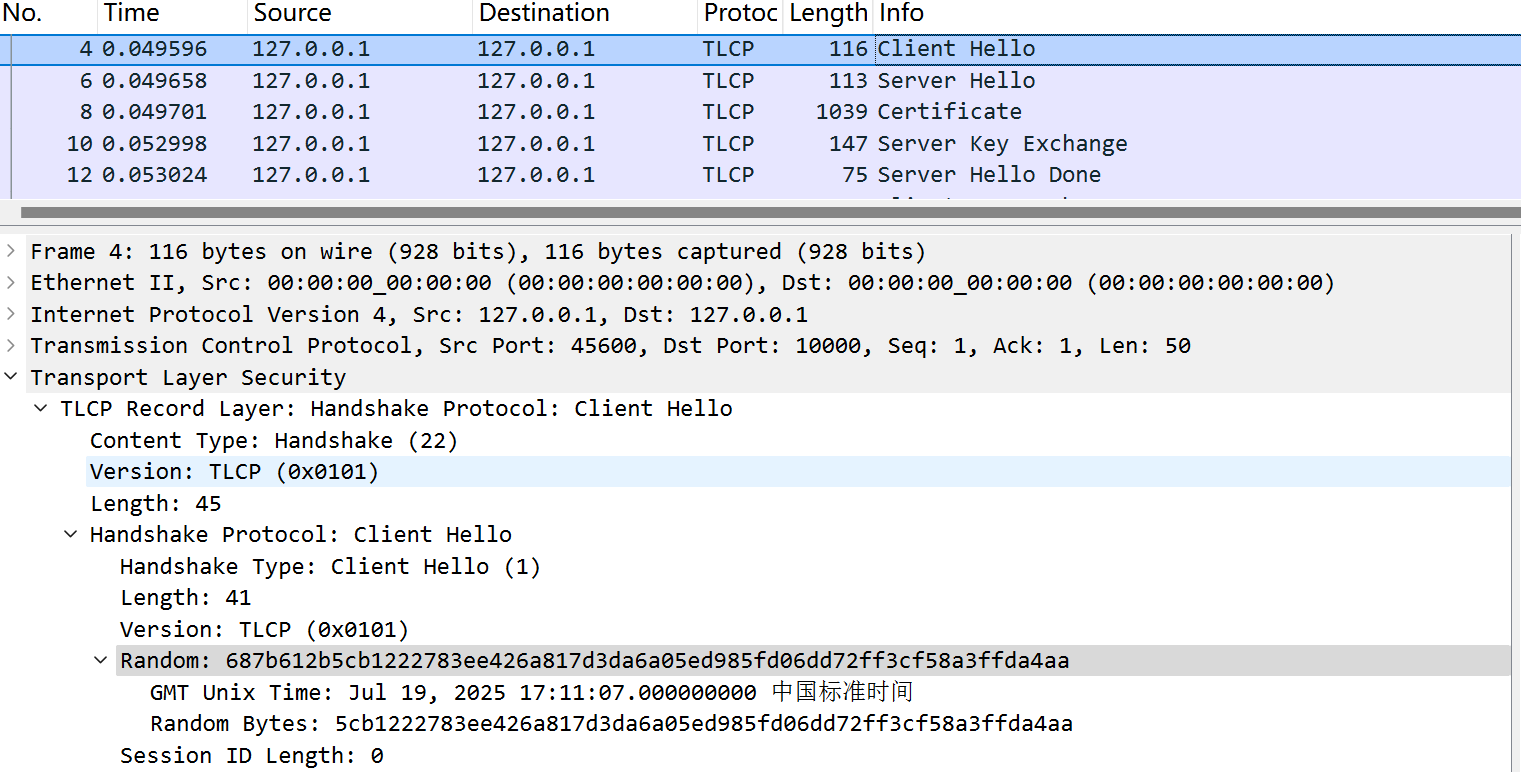 
这里会包含一个客户端生成的随机数，我们先把他记录下来，后续生成工作密钥会用到：
1
CR = "687b612b5cb1222783ee426a817d3da6a05ed985fd06dd72ff3cf58a3ffda4aa"
同样的，Server Hello消息也会包含一个服务端随机数，也记录下来：
1
SR = "687b612bdbd4517e6fc989ddd2bf25e78b5e21e576bbd8f46add6d7df527887f"
双方在交换随机数后，服务端会发来Certificate消息：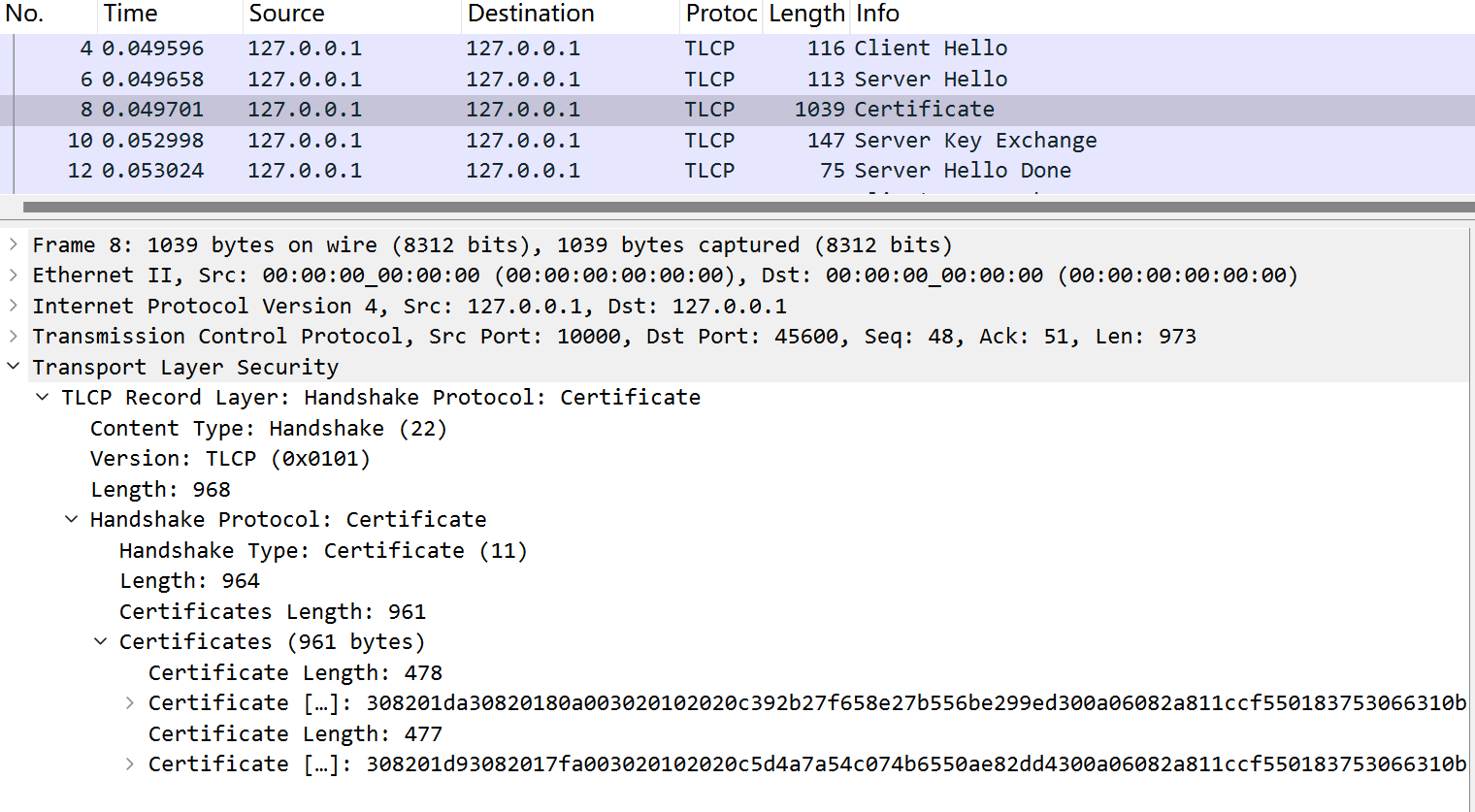 
这里面包含2个证书，第1个是签名证书，第2个是加密证书。
签名证书用来验证加密证书的有效性，加密证书用于后续的密钥交换。
签名证书的内容如下：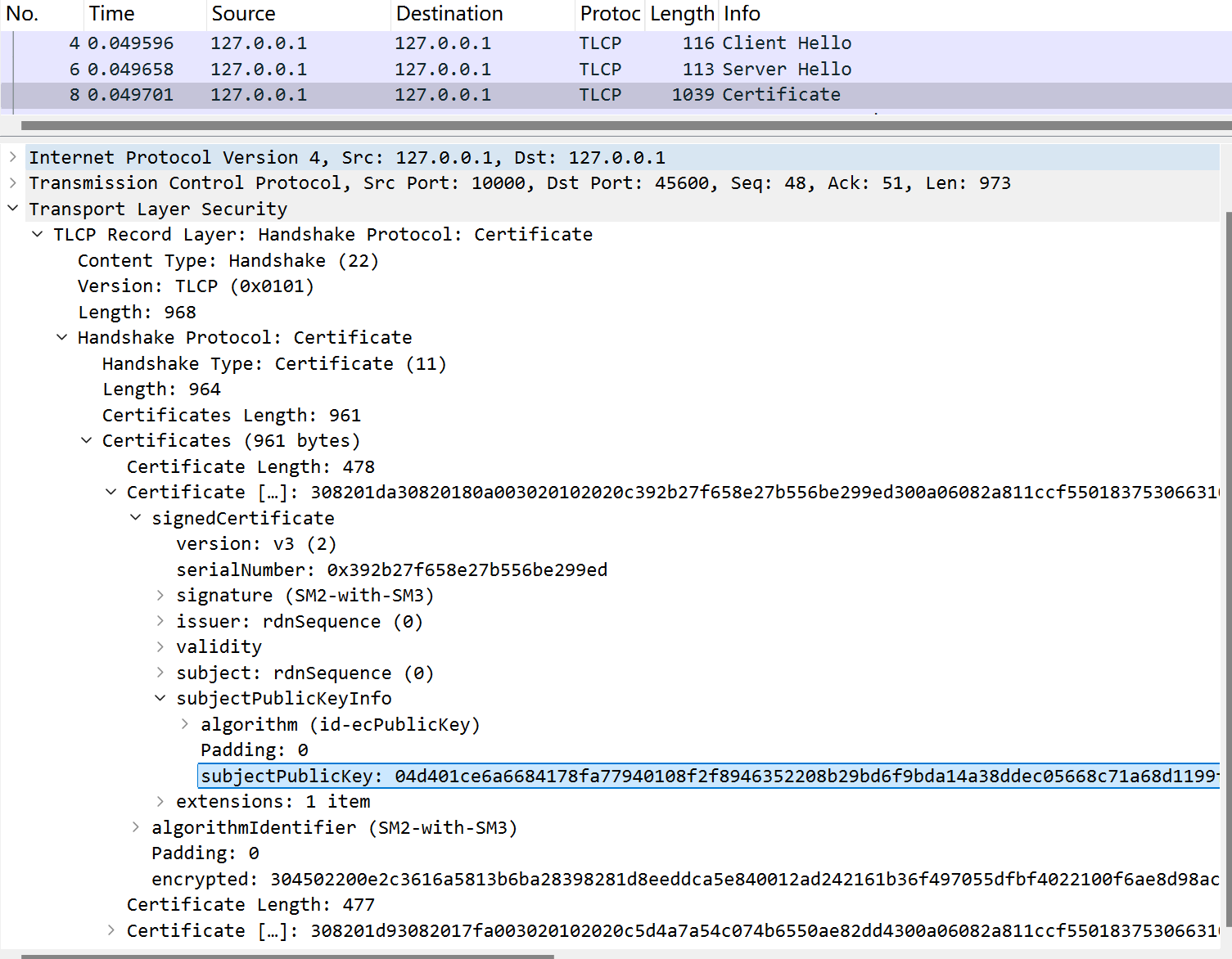 
其中subjectPublickey就是签名的公钥，把04的tag去掉，剩下的64字节就是公钥的横纵坐标：
1
2x = 0xd401ce6a6684178fa77940108f2f8946352208b29bd6f9bda14a38ddec05668c
y = 0x71a68d1199f376f5656e0d6fa93d73196e02c95ad2b311f9c220d3139ad0ccdc
签名值在Server Key Exchange消息中：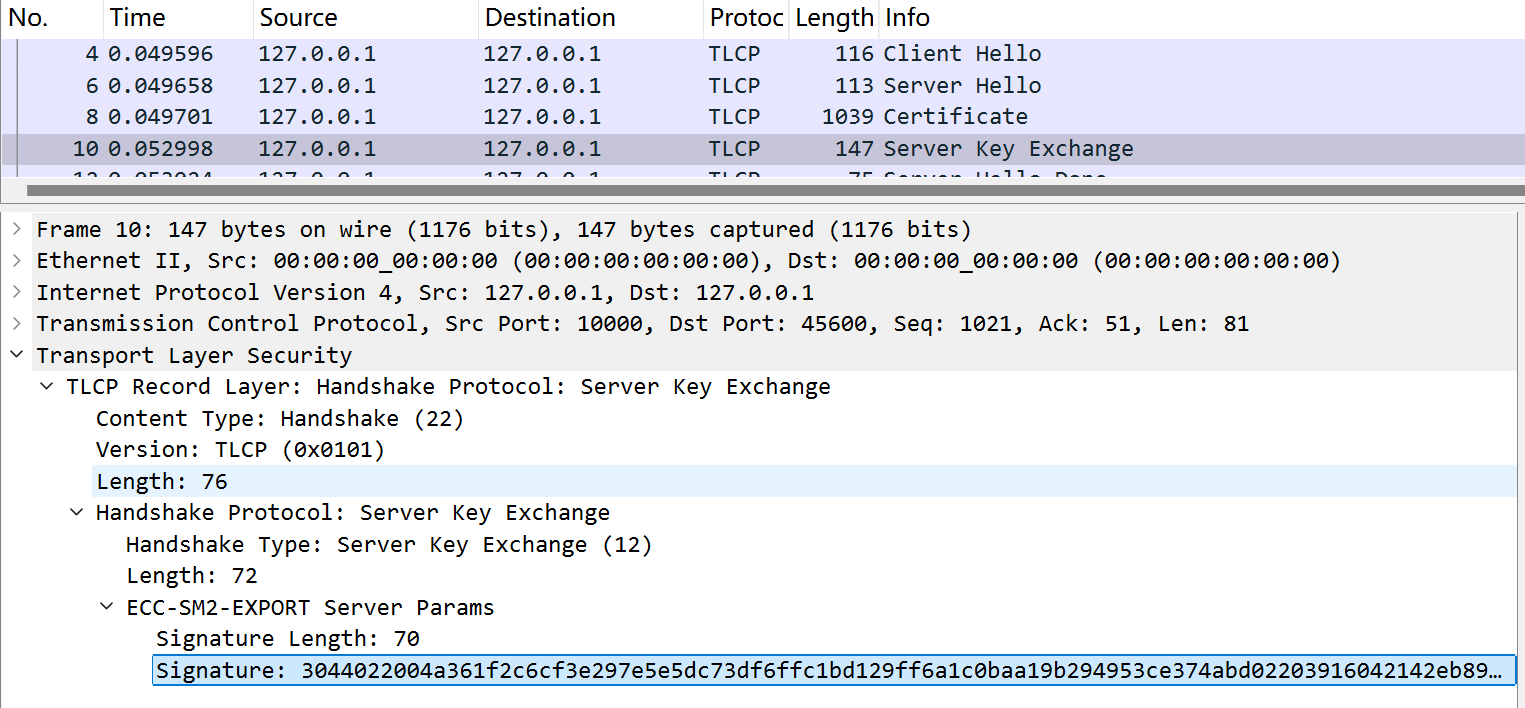 
按如下方式解析签名[6]：
签名值是： 1
2r = 0x04a361f2c6cf3e297e5e5dc73df6ffc1bd129ff6a1c0baa19b294953ce374abd
s = 0x3916042142eb8919763f7f304a48be1aaf02866e6935a30503c5d90e2f4c7927
拿到公钥和签名后，来看签名过程[2]： 
其中\(ID_A\)使用默认值[6]： 
消息\(M\)由客户端随机数、服务端随机数、加密证书拼接得到。在复制加密证书的时候，一定要把表示证书长度的3字节也复制上。
最后，拿到数据，我们可以验证一下： 1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38# verify.py
from gmssl import sm3
n = 0xFFFFFFFEFFFFFFFFFFFFFFFFFFFFFFFF7203DF6B21C6052B53BBF40939D54123
p = 0xFFFFFFFEFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFF00000000FFFFFFFFFFFFFFFF
g = (0x32c4ae2c1f1981195f9904466a39c9948fe30bbff2660be1715a4589334c74c7,
0xbc3736a2f4f6779c59bdcee36b692153d0a9877cc62a474002df32e52139f0a0)
a = 0xFFFFFFFEFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFF00000000FFFFFFFFFFFFFFFC
b = 0x28E9FA9E9D9F5E344D5A9E4BCF6509A7F39789F515AB8F92DDBCBD414D940E93
E = EllipticCurve(GF(p), [a, b])
G = E(g)
def verify(r, s, e, PubKey):
t = (s1 + r1) % n
P1 = s1 * G
P2 = t * PubKey
x = int((P1 + P2).x())
return (e1 + x - r1) % n == 0
ENTL_A = b"\x00\x80"
ID_A = b"1234567812345678"
a_byte = bytes.fromhex(hex(a)[2:].zfill(64))
b_byte = bytes.fromhex(hex(b)[2:].zfill(64))
xG = bytes.fromhex(hex(int(G.x()))[2:].zfill(64))
yG = bytes.fromhex(hex(int(G.y()))[2:].zfill(64))
PK = E(0xd401ce6a6684178fa77940108f2f8946352208b29bd6f9bda14a38ddec05668c, 0x71a68d1199f376f5656e0d6fa93d73196e02c95ad2b311f9c220d3139ad0ccdc)
CER = "0001dd308201d93082017fa003020102020c5d4a7a54c074b6550ae82dd4300a06082a811ccf550183753066310b300906035504061302434e3111300f0603550408130850524f56494e43453111300f060355040713084c4f43414c495459310c300a060355040a13034f52473110300e060355040b13074f524755494e543111300f060355040313084e65704e65704341301e170d3235303731333035313231345a170d3335303731313035313231345a3067310b300906035504061302434e3111300f0603550408130850524f56494e43453111300f060355040713084c4f43414c495459310c300a060355040a13034f52473110300e060355040b13074f524755494e5431123010060355040313094e65704e6570456e633059301306072a8648ce3d020106082a811ccf5501822d03420004b1e942c2068b9312f82cf22b5c01f4910e49e10408478c03ad9c5e37013852212f90f0d88d7e2ca86bb718772b213e757d0e6ca505444d19d5496c9a70323d46a3123010300e0603551d0f0101ff040403020520300a06082a811ccf55018375034800304502206671281fe2bf53d3c596132fe5a58101ec805566b5b76a5ac7b549fe5e4805c5022100cf148ffa42395c3a60cf103953fcf728d566080fced186c9191fef9b5f81e081"
xA = bytes.fromhex(hex(int(PK.x()))[2:].zfill(64))
yA = bytes.fromhex(hex(int(PK.y()))[2:].zfill(64))
ZA = sm3.sm3_hash(list(ENTL_A + ID_A + a_byte + b_byte + xG + yG + xA + yA))
CR = "687b612b5cb1222783ee426a817d3da6a05ed985fd06dd72ff3cf58a3ffda4aa"
SR = "687b612bdbd4517e6fc989ddd2bf25e78b5e21e576bbd8f46add6d7df527887f"
r1 = 0x04a361f2c6cf3e297e5e5dc73df6ffc1bd129ff6a1c0baa19b294953ce374abd
s1 = 0x3916042142eb8919763f7f304a48be1aaf02866e6935a30503c5d90e2f4c7927
M = ZA + CR + SR + CER
M = bytes.fromhex(M)
e1 = int(sm3.sm3_hash(list(M)), 16)
assert verify(r1, s1, e1, PK)
同样的，我们还可以获取第二个通信的签名，然后根据题目提示的随机数复用（随机数复用这一点，也可以通过比对两次签名的\((r - e) \mod
n\)值来发现），只需要解一个线性方程组来恢复签名的私钥：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21# get_sign_prikey.py
n = 0xFFFFFFFEFFFFFFFFFFFFFFFFFFFFFFFF7203DF6B21C6052B53BBF40939D54123
def sollin(r1, s1, r2, s2):
k, d = var("k d")
f1 = (1 + d) * s1 - k + r1 * d
f2 = (1 + d) * s2 - k + r2 * d
fd = f1.resultant(f2, k)
fk = f1.resultant(f2, d)
PR.<d> = PolynomialRing(GF(n))
fd = PR(str(fd))
d = int(fd.roots()[0][0])
PR.<k> = PolynomialRing(GF(n))
fk = PR(str(fk))
k = int(fk.roots()[0][0])
return k, d
r1 = 0x04a361f2c6cf3e297e5e5dc73df6ffc1bd129ff6a1c0baa19b294953ce374abd
s1 = 0x3916042142eb8919763f7f304a48be1aaf02866e6935a30503c5d90e2f4c7927
r2 = 0x604b0232ee0907c6957c1521457ff2ab5bb32a7637221eec88c0e7fba6fc4b12
s2 = 0x6c0e3e59b46bb87abf7c9c7398bc75bec795e85e92c2414770772ea32a0b8205
k, d = sollin(r1, s1, r2, s2)
print(f"{d = }")1
d = 56431408153695370061795421010209097251225434679562598847096735820032467303653
解密通信流量
首先需要获取预主密钥（48字节），前2字节是0x0101（客户端所支持的版本号），后46字节是随机数。预主密钥由客户端生成，并在Client Key Exchange消息中通过加密证书加密传输。
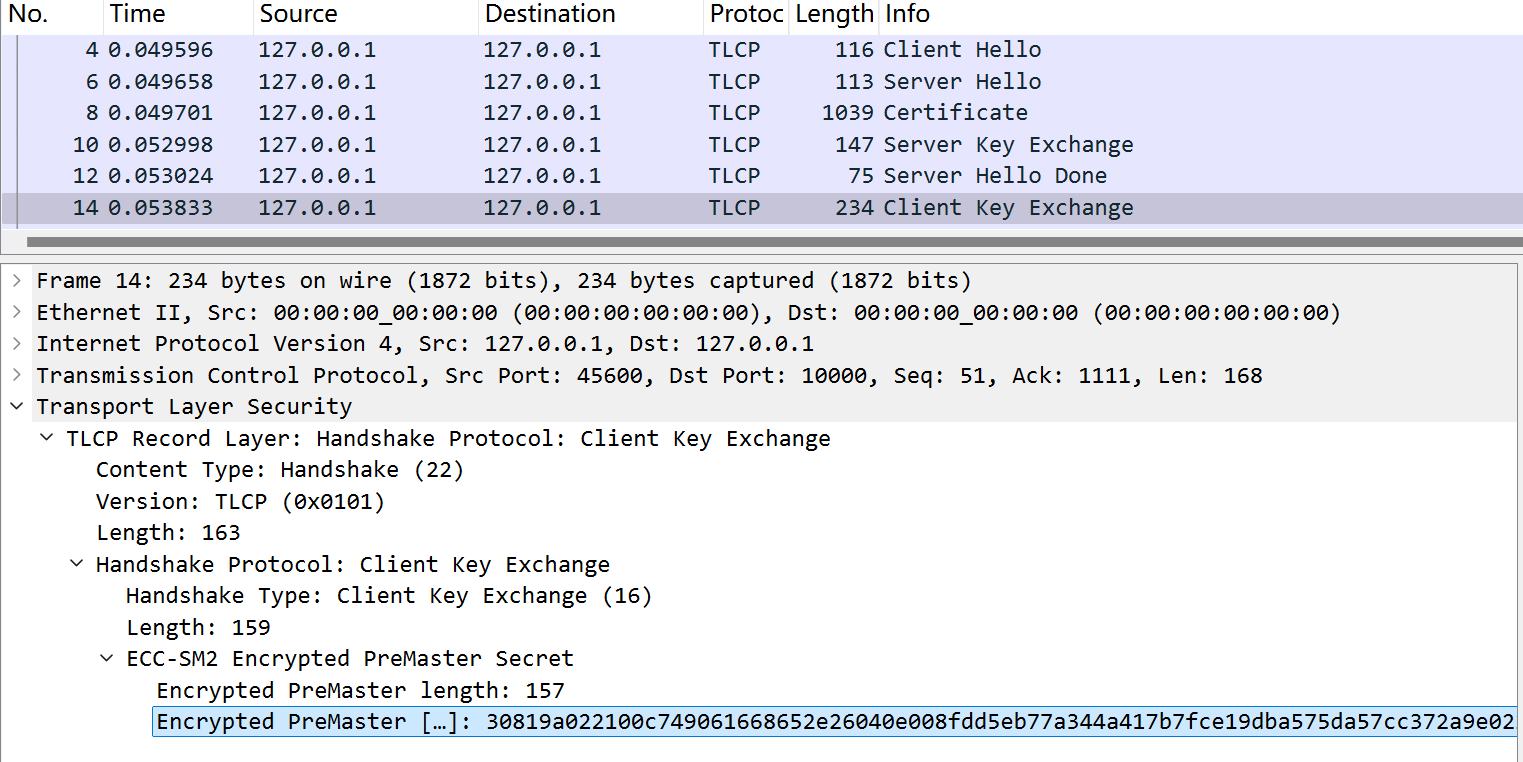
密文可以按如下结构解析[6]：
得到： 1
2
3
4x = 0x00c749061668652e26040e008fdd5eb77a344a417b7fce19dba575da57cc372a9e
y = 0x00f2df5db2d144e9454504c622b51cf38f5006206eb579ff7da6976eff5fbe6480
h = "d682849ee64d092a590e0a981d750a608e59d08fdc9511426aa90b99e7c215c7"
c = "67ec55ae9437abdf46ee8a1406a3356c2123b598d92a2980d7dab8ec1a51fb9d7c987b2f7d16dcf9da95ea2c86875191"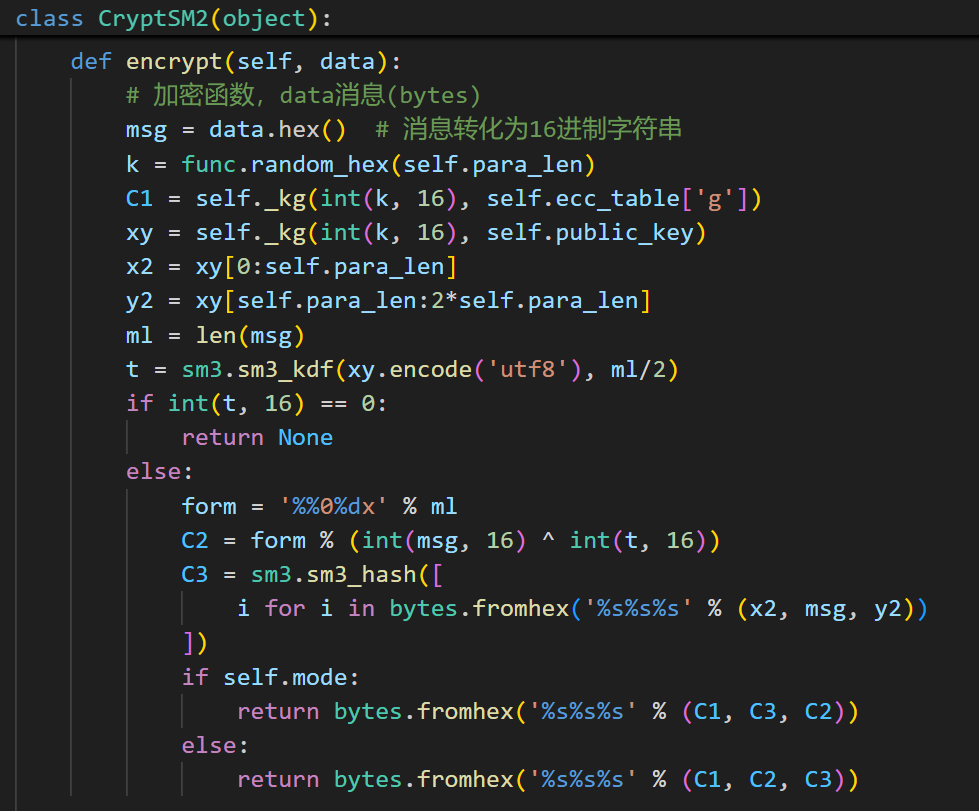
可以发现，当使用相同的随机数时，最终生成的异或密钥也会相同，这样就可以通过数据库中已知的明密文，获取异或密钥，然后解密上面的密文获得预主密钥。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15def xor_bytes(a, b):
return bytes([i ^ j for i, j in zip(a, b)])
db_plain = "4e475132595451784e7a6b305a5455314d7a5532597a597a4e44637a4e545a6a4e6a4d304e54526c4e5455314d6a"
db_cipher = "28AA2529E18960E93052D856ED1D1476B19FE04367EDAAD6E2F177AD7DE0F9B04B2C8C98EAC83397DA0CDEB7E281"
db_plain = bytes.fromhex(db_plain)
db_cipher = bytes.fromhex(db_cipher)
xor_key = bytes([i^j for i, j in zip(db_plain, db_cipher)])
enc_pre_secret = "67ec55ae9437abdf46ee8a1406a3356c2123b598d92a2980d7dab8ec1a51fb9d7c987b2f7d16dcf9da95ea2c86875191"
enc_pre_secret = bytes.fromhex(enc_pre_secret)
pre_secret_prefix = xor_bytes(enc_pre_secret, xor_key)
assert len(pre_secret_prefix) == 46
print(pre_secret_prefix.hex())
# 010121b52cea9a4e38c63972b1ea742bddc600e9e7bdda2c7b6fac3b29e5584779deba87d98abd024ecd61aa296c
由于数据库中已知明密文长度都是46字节，所以我们只拿到了预主密钥的前46字节，还需要爆破2字节。
拿到预主密钥后，根据如下方法生成主密钥[7]： 
PRF函数定义如下[7]： 
获取到主密钥后，再获取工作密钥[7]： 
这些密钥长度分别是32、32、16、16、16、16。
在双方成功获取到工作密钥后，都会发送一个Finished消息，在wireshark中显示为Encrypted Handshake Message：
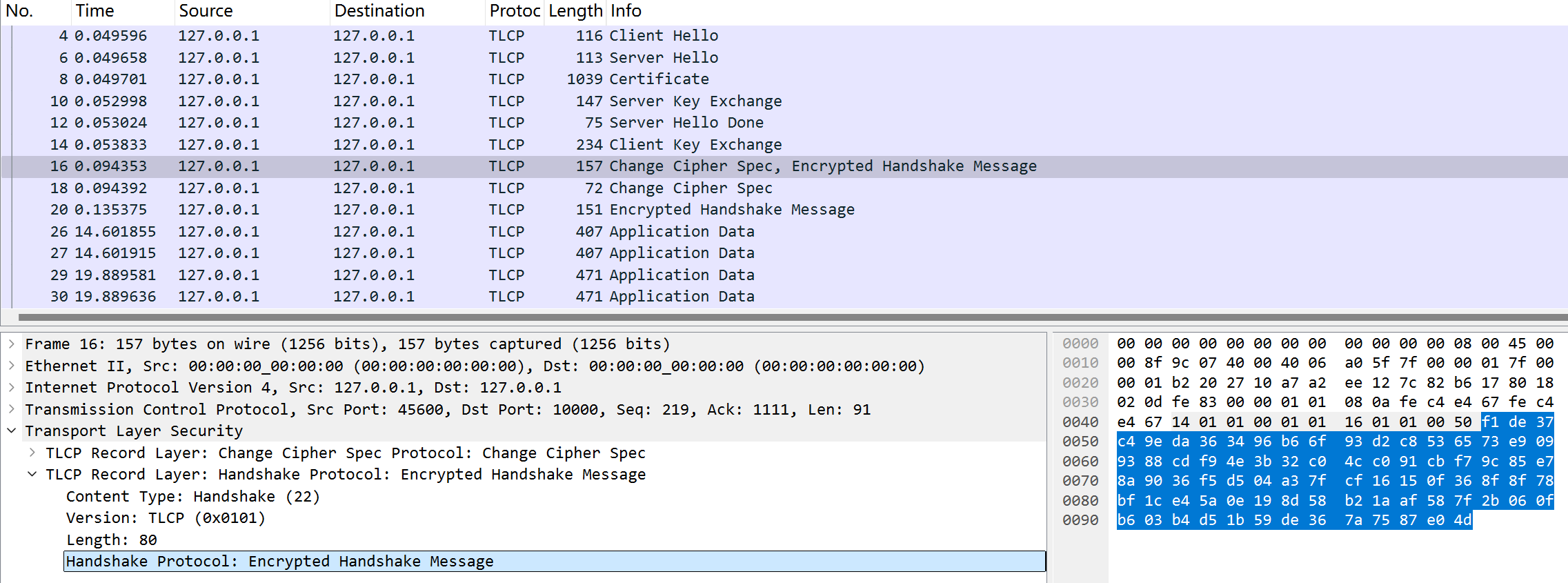
我们先来看客户端发送的这个消息，长度80字节（16字节IV+cipher（16字节finished消息明文+32字节MAC+16字节的padding））[10]： 1
f1de37c49eda363496b66f93d2c8536573e9099388cdf94e3b32c04cc091cbf79c85e78a9036f5d504a37fcf16150f368f8f78bf1ce45a0e198d58b21aaf587f2b060fb603b4d51b59de367a7587e04d
解析得： 1
2
3
4iv = "f1de37c49eda363496b66f93d2c85365"
finished_cipher = "73e9099388cdf94e3b32c04cc091cbf7"
mac_cipher = "9c85e78a9036f5d504a37fcf16150f368f8f78bf1ce45a0e198d58b21aaf587f"
padding_cipher = "2b060fb603b4d51b59de367a7587e04d"1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82# brute_pre_secret.py
from gmssl import sm2, sm3, sm4
from tqdm import trange
def SM3(msg: bytes):
return bytes.fromhex(sm3.sm3_hash(list(msg)))
def HMAC(key: bytes, message: bytes):
if isinstance(key, str):
key = key.encode('utf-8')
if isinstance(message, str):
message = message.encode('utf-8')
block_size = 64
if len(key) > block_size:
key = bytes.fromhex(sm3.sm3_hash(list(key)))
if len(key) < block_size:
key += b'\x00' * (block_size - len(key))
ipad = b'\x36' * block_size
opad = b'\x5c' * block_size
inner_key = bytes([k ^ i for k, i in zip(key, ipad)])
inner_data = inner_key + message
inner_hash = sm3.sm3_hash(list(inner_data))
outer_key = bytes([k ^ o for k, o in zip(key, opad)])
outer_data = outer_key + bytes.fromhex(inner_hash)
outer_hash = sm3.sm3_hash(list(outer_data))
return bytes.fromhex(outer_hash)
def P_hash(secret: bytes, seed: bytes, len: int):
A = seed
result = b""
for _ in range(len // 32):
A = HMAC(secret, A)
result += HMAC(secret, A + seed)
A = HMAC(secret, A)
result += HMAC(secret, A + seed)[:len % 32]
return result
def PRF(secret, label, seed, len):
return P_hash(secret, label + seed, len)
def xor_bytes(a, b):
return bytes([i ^ j for i, j in zip(a, b)])
db_plain = "4e475132595451784e7a6b305a5455314d7a5532597a597a4e44637a4e545a6a4e6a4d304e54526c4e5455314d6a"
db_cipher = "28AA2529E18960E93052D856ED1D1476B19FE04367EDAAD6E2F177AD7DE0F9B04B2C8C98EAC83397DA0CDEB7E281"
db_plain = bytes.fromhex(db_plain)
db_cipher = bytes.fromhex(db_cipher)
xor_key = bytes([i^j for i, j in zip(db_plain, db_cipher)])
print(f"{xor_key = }")
CR = "687b612b5cb1222783ee426a817d3da6a05ed985fd06dd72ff3cf58a3ffda4aa"
SR = "687b612bdbd4517e6fc989ddd2bf25e78b5e21e576bbd8f46add6d7df527887f"
CR = bytes.fromhex(CR)
SR = bytes.fromhex(SR)
enc_pre_secret = "67ec55ae9437abdf46ee8a1406a3356c2123b598d92a2980d7dab8ec1a51fb9d7c987b2f7d16dcf9da95ea2c86875191"
enc_pre_secret = bytes.fromhex(enc_pre_secret)
pre_secret_prefix = xor_bytes(enc_pre_secret, xor_key)
assert len(pre_secret_prefix) == 46
iv = bytes.fromhex("f1de37c49eda363496b66f93d2c85365")
c = bytes.fromhex("73e9099388cdf94e3b32c04cc091cbf7")
for i in trange(256 * 256 - 1, 0, -1):
pre_secret = pre_secret_prefix + bytes.fromhex(hex(i)[2:].zfill(4))
master_secret = PRF(pre_secret, b"master secret", CR + SR, 48)
ALL_KEY = PRF(master_secret, b"key expansion", SR + CR, 80)
ck = ALL_KEY[64: 64 + 16]
SM4 = sm4.CryptSM4()
SM4.set_key(ck, sm4.SM4_DECRYPT)
# 这里只解密了16字节，结果肯定不满足PKCS#7的填充方式，SM4.crypto_cbc会返回空，所以最好直接把源码里面的去填充部分去掉
pt = SM4.crypt_cbc(iv, c)
if pt[:4] == b"\x14\x00\x00\x0c":
print(f"{pre_secret = }")
break
# pre_secret = b'\x01\x01!\xb5,\xea\x9aN8\xc69r\xb1\xeat+\xdd\xc6\x00\xe9\xe7\xbd\xda,{o\xac;)\xe5XGy\xde\xba\x87\xd9\x8a\xbd\x02N\xcda\xaa)l\xf7B'
拿到预主密钥后，再按照上面的方法，生成工作密钥，就可以解密Application Data消息中的密文了。
最后的SM2
拿到工作密钥后，我解密了第一个Application Data中的密文，解密结果为：
1
2
3
4b'\xb3K\x9a\xe3z\x124Y{\xf2\x9a^[\xa5ck308189022100D41161C94F626297DB5CAE9D1B1ABC1C6363064DA2D82C48F0DDF7F8B98966D102204AEC64B7742E5C014665BCB9BD1AEFB4BE973854929DA50F23B583D2CC283DD90420F19E80E48A53140E33178DC48F9195E6D87463608464E64AF47C0DF58A3B083104208D4C762D5BAF59B6787B11DB97A4129B44CEE3BE7782D5A35A7FA57F59089089\n\x90)\xd7\x00\x05\x1fe\xc7\x9d\xb8\xea\xddcG)\xc4\xee\x81\xcf\x18\xf5\xeb\xf5\xea\x8a\xc9g\xee\x18\xd5O\xc6\x06\x06\x06\x06\x06\x06\x06'
b'b\xf5\xdc#\x91\xcbEL\xe0\xf0$\xd72H\x07\xd33081AA02201169369B36F4266E9A86007020B8917DEE190E7F3323BA889FE4FD9423EB39CE02210099ADDE8DC3128E6FE4521A2E1740AD73A570FB7F5D289435E71E47218BEC28010420957B7D29A5734EB548E03E5E0A4A2CA87CE493D5E6908503D7D36881C71F09A30441B111A30786E760723E744718DF10E4E33CA0D7003FB7A0A4EE37226586D2F7B7A3BB9A8D35134C39192B3735FA76C3562CC3E3E158F40ED83BBF321387B8A65848\n\xbc\xd5A\xcd\x7f@Rh\x81\x99\xeaK\x9a\xfe\x02\xea\xc9\x8f\x8b\xb2\xf3\xee\x80\x1b[ZG\xc4\xaa\xf8?\xec\x04\x04\x04\x04\x04'
b't\xc1\xe6[\xcbY\x94NH\xf1\xdb\x8d\xcc\xb0\x97\xf330819202203F271466AE70B4B61C660B3E727BAB30FA988751F771F4380E3ED95A706979CC022100D23C2B2662E8AFA757F136B47116DB9F52A05EF2FD7F7326D08FE113B9E9EA79042061D6AFB6D97BD62119D3E90527A093AEE6A059A015B20960BF7574F1CAA39D4C0429FB2E3155BA0383D07CFE0D866E73DBB890B2DA037F07BA5D2A0D7E2CDAAECEF91DD4E169DB8412245C\n\x9e\xd3\xa2\xb9\x06\xbb\x0f\xd5o\xdb\x03\xee\x93\x84\x00\x8a\xc4\x98\x1d]q\x87?\x96f\xa8\rvH\x1b\xfa\xba\x04\x04\x04\x04\x04'
b"v\xf7\xc0O\xd9\x14\xb5\x08'\x17j\xe9\x89\xcc\x8b`308199022100C749061668652E26040E008FDD5EB77A344A417B7FCE19DBA575DA57CC372A9E022100F2DF5DB2D144E9454504C622B51CF38F5006206EB579FF7DA6976EFF5FBE64800420CD0DF57ACF39667C8E3BD5C16B9381DEAB56A2CE696A3ACE83E4D189AD98964A042F51D4412F8CBF06F3494D8500D32F70229FD381170BA690CD9BD376B55580C6E33523F79D9DA9519FF668EFB29888AC\n\x13\n\x1f\xdfjGh\xfc\x89Q\x9ez2\x0eD\xd5\xc0LC\xee\xe0\xed\xb6W\xa9\xde\x9c\x08)\x08\xe6\xc8\x06\x06\x06\x06\x06\x06\x06"
唯一不同的是最后一次TLCP通信，里面的Application Data消息解密后剩下的SM2密文，没法在数据库表中找到对应密钥，所以没法解密。这个时候我又去问了问出题人，了解到了最后一次SM2加密的随机数，其实用的是前面签名证书的私钥，知道了这一点后，就很快解密了数据，成功拿到flag。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18# final.py
from gmssl import sm3
n = 0xFFFFFFFEFFFFFFFFFFFFFFFFFFFFFFFF7203DF6B21C6052B53BBF40939D54123
p = 0xFFFFFFFEFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFF00000000FFFFFFFFFFFFFFFF
a = 0xFFFFFFFEFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFF00000000FFFFFFFFFFFFFFFC
b = 0x28E9FA9E9D9F5E344D5A9E4BCF6509A7F39789F515AB8F92DDBCBD414D940E93
E = EllipticCurve(GF(p), [a, b])
d = 56431408153695370061795421010209097251225434679562598847096735820032467303653
x = 0xde11a990ff68085d48d482ebc43f69806843810d57e89b348e052406d33ec1c2
y = 0x197f651f724edd26b43f283569c117b8586d2e0278f8b1fbb64f9247e08d0ca7
cipher = bytes.fromhex("8ffd6249f3e6733945100a05b0893e2d9290173f1101c3b2f0a7eb618464d2b594ea09f5")
PK = E((x, y))
S = d * PK
Sx = hex(int(S.x()))[2:].zfill(64)
Sy = hex(int(S.y()))[2:].zfill(64)
t = bytes.fromhex(sm3.sm3_kdf((Sx + Sy).encode(), len(cipher)))
flag = bytes([i^^j for i, j in zip(t, cipher)])
print(flag)1
NepCTF{Y0u_A1e_900D_at_TLCP_And_SM_A1g0r1tm}